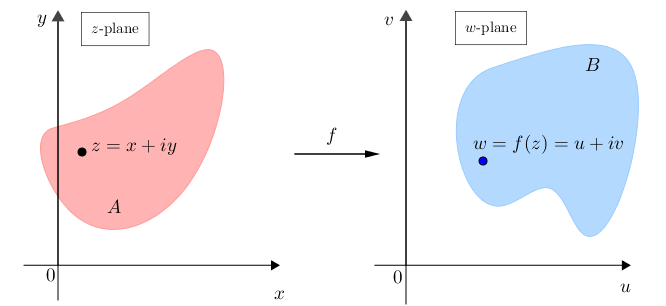
A complex function $w = f (z)$ can be regarded as a mapping or transformation of the points in the $z = x + iy $ plane to the points of the $w = u + iv$ plane. In real variables in one dimension, this notion amounts to understanding the graph $y = f (x)$, that is, the mapping of the points $x$ to $y = f (x)$.
In complex variables the situation is more difficult due to the fact that we have four dimensions. Thus a graphical depiction such as in the real one-dimensional case is not feasible. Rather, one considers the two complex planes, $z$ and $w$, separately and asks how a region in the $z$ plane transforms or maps to a corresponding region or image in the $w$ plane.
Things to try:
The University of Queensland