SciMS - Numerical Analysis The University of Queensland

Approximation theory

Trigonometric approximation: Cosine and Sine series

The Fourier cosine and sine series can be used to approximate functions. In particular, if $f$ is a function defined on the interval $\left(0,\pi\right)$, then the cosine series approximation of $f$ is \[ f(x)=\frac{a_0}{2}+\sum_{n=1}^\infty a_n \cos(n x), \] where \begin{eqnarray*} a_0 & = & \frac{2}{\pi} \int_0^{\pi} f(x)dx\\ a_n & = & \frac{2}{\pi} \int_0^{\pi} f(x) \cos(n x) dx. \end{eqnarray*}

On the other hand, the sine series approximation of $f$ is \[ f(x)=\sum_{n=1}^\infty b_n \sin(n x), \] where \begin{eqnarray*} b_n & = & \frac{2}{\pi} \int_0^{\pi} f(x) \sin(n x) dx. \end{eqnarray*}

Orthogonal polynomials and least squares approximation

To discuss general function approximation requires the introduction of the notions of weight functions and orthogonality.

Definition: An integrable function $w$ is called weight function on the interval $I$ if $w(x)\geq 0$, for all $x\in I$, but $w(x)\neq 0$ on any subinterval of $I$.

Suppose $\{\phi_0,\phi_1,\ldots,\phi_n\}$ is a set of linearly independent functions on $[a,b]$ and $w$ is a weight function for $[a,b]$. Given $f\in C[a,b]$, we seek a linear combination $$P(x)=\sum_{k=0}^n a_k \phi_k(x)$$ to minimise the error

$$E=E(a_0,a_1,\ldots,a_n)=\int_a^b w(x)\left[f(x)-\sum_{k=0}^n a_k \phi_k(x)\right]^2dx.$$

Definition: The set $\{\phi_0,\phi_1,\ldots,\phi_n\}$ is said to be an orthogonal set of functions for the interval $[a,b]$ with respect to the weight function $w$ if

$$\int_a^b w(x) \phi_k(x) \phi_j(x) dx= \begin{cases} 0, & \text{when } j \neq k, \\ \alpha_j > 0, & \text{when } j = k. \end{cases}$$
If, in addition, $\alpha_j=1$ for each $j=0,1,\ldots,n$, the set is said to be orthonormal.

Theorem: If $\{\phi_0,\phi_1,\ldots,\phi_n\}$ is an orthogonal set of functions on the interval $[a,b]$ with respect to the weight function $w$, then the least squares approximation to $f$ on $[a,b]$ with respect to $w$ is $$P(x)=\sum_{j=0}^n a_j \phi_j(x),$$ where, for each $j=0,1,\ldots,n,$

$$a_j=\frac{\int_a^b w(x) \phi_j(x) f(x) dx}{\int_a^b w(x) \left[\phi_j(x)\right]^2 dx}=\frac{1}{\alpha_j}\int_a^b w(x) \phi_j(x) f(x) dx.$$

Legendre polynomials

The Legendre polynomials $P_n(x)$ are solutions to the Legendre differential equation:

\begin{eqnarray*} \frac{d}{dx}\left[(1-x^2)\frac{dy}{dx}\right]+l(l+1)y=0. \end{eqnarray*}
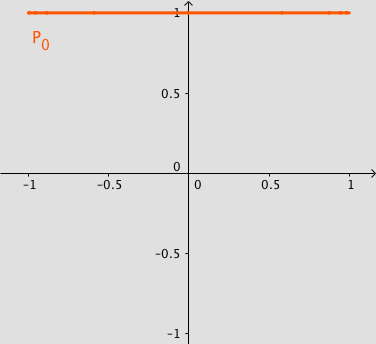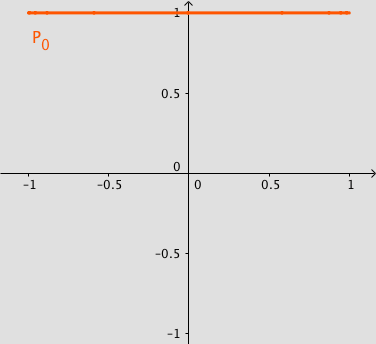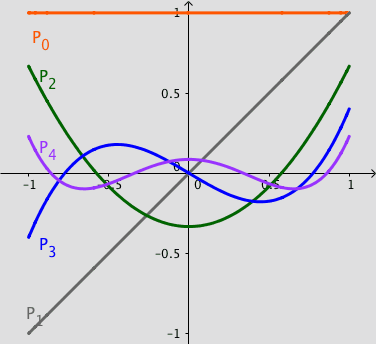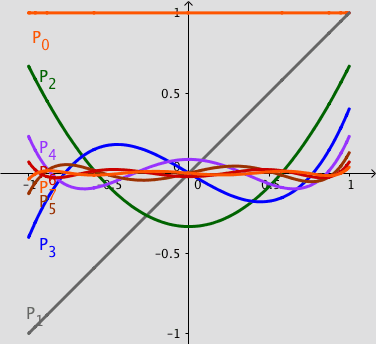
These polynomials can be generated using the Gram-Schmidt process. For example, the first five Legendre polynomials are:
\begin{eqnarray*} P_0(x)&= &1\\ P_1(x)&= &x\\ P_2(x)&= &x^2 - \frac{1}{3}\\ P_3(x)&= &x^3 - \frac{3}{5} x\\ P_4(x)&= &x^4 - \frac{6}{7} x^2 + \frac{3}{35}\\ P_5(x)&= &x^5 - \frac{10}{9} x^3 + \frac{5}{21} x \end{eqnarray*}
Some Legendre polynomials are illustrated in Figure 1.

Legendre polynomials
Figure 1: Legendre polynomials.

Chebyshev polynomials

The Chebyshev polynomials $T_n(x)$ are solutions to the Chebyshev differential equation:

\begin{eqnarray*} (1-x^2)\frac{d^2y}{dx^2}-x\frac{dy}{dx}+\alpha^2y=0. \end{eqnarray*}
Chebyshev polynomials can also be generated using the Gram-Schmidt process. For example, the first five polynomials are:
\begin{eqnarray*} T_0(x)&= &1\\ T_1(x)&= & x\\ T_2(x)&= &2 x^2 - 1\\ T_3(x)&= & 4x^3 - 3x\\ T_4(x)&= & 8x^4 - 8x^2 +1\\ T_5(x)&= & 16x^5 - 20x^3 + 5x \end{eqnarray*}
Some Chebyshev polynomials are illustrated in Figure 2.

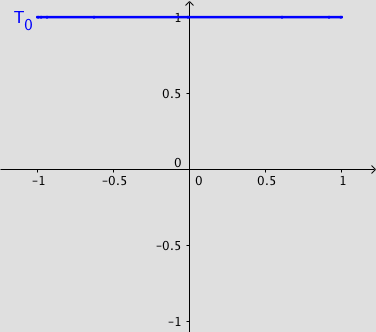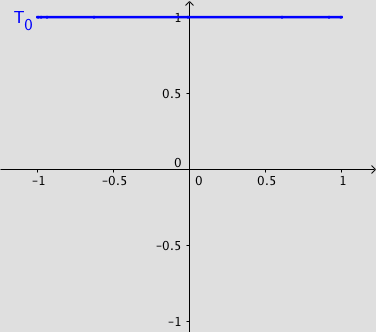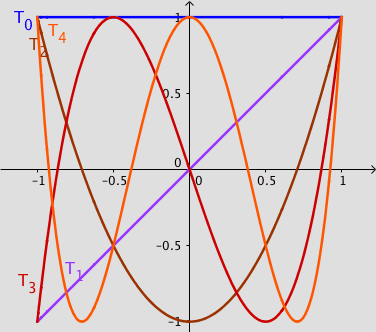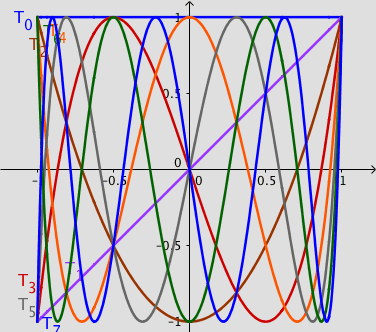
Chebysheb polynomials
Figure 2: Chebysheb polynomials.

Since the Legendre and Chebyshev polynomials are orthogonal functions on the interval $[-1,1]$ with respect to the weights functions

\[ w(x)=1 \qquad \text{and}\qquad w(x)=\frac{1}{\sqrt{1-x^2}}, \]
respectively; they can be used to approximate functions defined on the interval $[-1,1]$.

Simulation

The following simulation shows partial sums of least squares approximations of continuous functions using:

Things to try:

Remark: Notice that the approximation is INCORRECT since the first three coefficients are zero by default in the simulation. Calculate the CORRECT coefficients, rounded to two decimals places, and enter these values in the simulation.

For example, the Legendre approximation of the default function $0.7|x|$ are: $a_0=0.35$, $a_1=0$, $a_2=0.66$. Type these values in the simulation.

Sorry, the simulation is not supported for small screens.


Open separate tab Download

Worksheet exemplar

The following file contains activities and problems associated with the simulations.

References