Taylor series in two dimensions

One-dimensional Taylor series

Let $a\in \mathbb R$ and $f(x)$ be and infinitely differentiable function on an interval $I$ containing $a$. Then the one-dimensional Taylor series of $f$ around $a$ is given by

\[ f(x)=f(a)+f'(a)(x-a)+\frac{f''(a)}{2!}(x-a)^2+\frac{f^{(3)}(a)}{3!}(x-a)^3+\cdots \]

which can be written in the most compact form:

\[ f(x)=\sum_{n=0}^{\infty} \frac{f^{(n)}(a)}{n!}(x-a)^n. \]

Recall that, in calculus, Taylor's theorem gives an approximation of a $k$-times differentiable function around a given point by a $k$-th order Taylor polynomial.

For example, the best linear approximation for $f(x)$ is $$f(x)\approx f(a)+f'(a)(x-a).$$ This linear approximation fits $f(x)$ with a line through $x=a$ that matches the slope of $f$ at $a$.

For a better approximation we can add other terms in the expansion. For instance, the best quadratic approximation is

$$f(x)\approx f(a)+f'(a)(x-a)+\frac12 f''(a)(x-a)^2.$$

Figure 1 shows the partial sums (up to 10 terms) of the Taylor series for the function $f(x)=1/(1+x^2)$ around $a=0.67$.

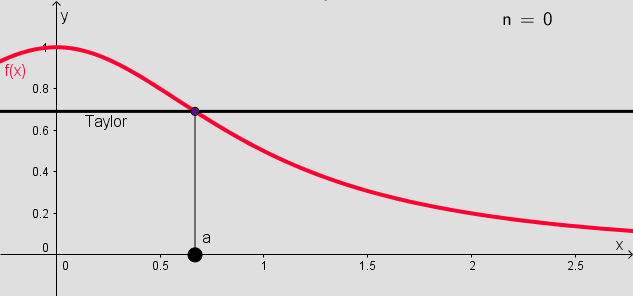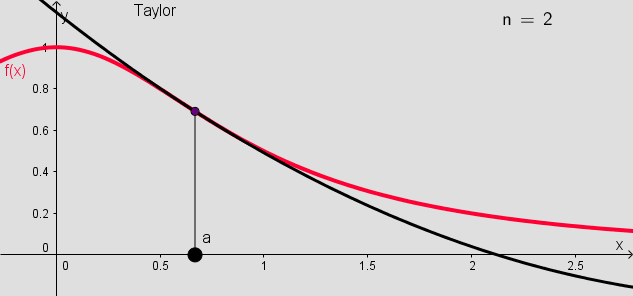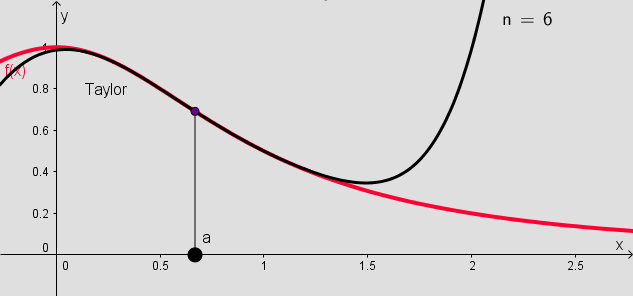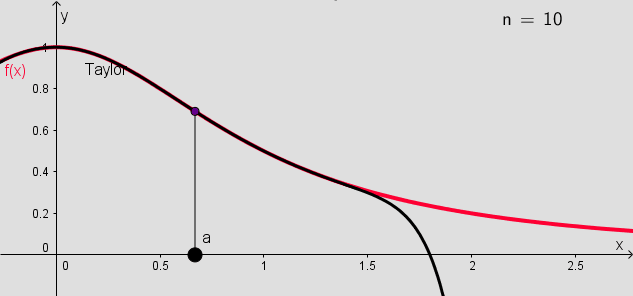
The Taylor series can be extended to calculate linear and quadratic approximations of functions of two variables.

Linear and Quadratic approximations using Two-dimensional Taylor series

In general, the two-dimensional Taylor series of $f(x,y)$ around a point $(a,b)$ is given by:

\begin{eqnarray*} f(x, y) & = &f(a, b) + f_x(a, b)(x - a) + f_y(a, b)(y - b)\\& &+\frac{1}{2!}\Big[f_{xx}(a, b)(x - a)^2 + 2f_{xy}(a, b)(x - a)(y - b) + f_{yy}(y - b)^2\Big]+\cdots \end{eqnarray*}

In this case, the best linear approximation to $f(x,y)$ around the point $(a,b)$ is

$$f(x,y) \approx L(x,y) = f(a,b) + f_x(a,b)(x-a) + f_y(a,b)(y-b).$$

On the other hand, the best quadratic approximation to $f(x,y)$ around the point $(a,b)$ is

\begin{eqnarray*} f(x, y) \approx Q(x,y) & = &f(a, b) + f_x(a, b)(x - a) + f_y(a, b)(y - b)\\& &+\frac{f_{xx}(a,b)}{2}(x-a)^2 + f_{xy}(a,b)(x-a)(y-b) + \frac{f_{yy}(a,b)}{2}(y-b)^2. \end{eqnarray*}

Simulation

The following simulation shows linear and quadratic approximations of functions of two variables.

Things to try:

Change the function f(x,y).
Example 1: 1/2x^2-1/2y^2
Example 2: y^2(1-xy)
Drag the point A to change the approximation region on the surface.
Select the approximation: Linear, Quadratic or Both.

Sorry, the simulation is not supported for small screens.

Open separate tab Download

Worksheet exemplar

The following file contains activities and problems associated with the simulation.